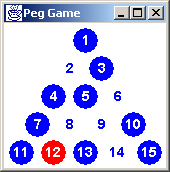
 The Peg Game consists of fifteen holes arranged in a triangle, and
fourteen pegs. The object is to remove pegs by jumping until one peg
remains. A "jump" consists of: finding two pegs and a hole in a row
(either horizontally or diagonally), jumping the outer peg over the
inner peg and into the hole, removing the jumped peg. It is all too
easy to run out of jumps before you run out of pegs. Leaving five pegs
on the board is below average, while three pegs is fairly average. The
player chooses where the empty hole is positioned before play is
begun.
The Peg Game consists of fifteen holes arranged in a triangle, and
fourteen pegs. The object is to remove pegs by jumping until one peg
remains. A "jump" consists of: finding two pegs and a hole in a row
(either horizontally or diagonally), jumping the outer peg over the
inner peg and into the hole, removing the jumped peg. It is all too
easy to run out of jumps before you run out of pegs. Leaving five pegs
on the board is below average, while three pegs is fairly average. The
player chooses where the empty hole is positioned before play is
begun.
> java PegGameDos
<A>
<B> <C>
<D> <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Select initial hole: a
a
<B> <C>
<D> <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Move (from to): d a
<A>
b <C>
d <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Move (from to): f d
<A>
b <C>
<D> e f
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Move (from to):
The next chapter will do for this puzzle what the previous chapter did for the Fifteen Puzzle.
Three iterations:
> java PegGameDos
<A>
<B> <C>
<D> <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
>
Instructions and issues:
> java PegGameDos
<A>
<B> <C>
<D> <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Remove: d
<A>
<B> <C>
d <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Remove: f
<A>
<B> <C>
d <E> f
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Instructions and issues:
<A>
<B> <C>
<D> <E> <F>
<G> <H> <I> <J>
<K> <L> <M> <N> <O>
Select initial hole: i
<A>
<B> <C>
<D> <E> <F>
<G> <H> i <J>
<K> <L> <M> <N> <O>
Move (from to): g i
<A>
<B> <C>
<D> <E> <F>
g h <I> <J>
<K> <L> <M> <N> <O>
Move (from to): j h
<A>
<B> <C>
<D> <E> <F>
g <H> i j
<K> <L> <M> <N> <O>
Move (from to):
Instructions and issues:
(char)('A' + i)
The choice made in listing 4.1 was to exercise Java's support for the
increment operator on a char variable.Notice how the number of iterations of the inner loop is controlled by the loop control variable of the outer loop.
for (int row=0; row < 5; row++) {
...
for (int column=0; column <= row; column++)
The indentation for each row could be implemented using the following
array of five blank strings.
private static String[] blanks = {" "," "," "," ",""};
...
for (int row=0; row < 5; row++) {
System.out.print( blanks[row] );
The choice made in listing 4.1 was to minimize the amount of storage
used, and compute the correct size blank string each iteration. The
String class in Java's standard library has two forms. The one used
here is substring( beginIndex ). As the variable row increases, the
amount of indentation decreases.
for (int row=0; row < 5; row++) {
System.out.print( blanks.substring( row*3 ) );
The first alternative above relies on the use of memory, or storage.
The second uses considerably less storage, but requres more
instructions, or processing. Very often, a choice must be made between
"store versus compute". The former incurs more memory overhead and
less overhead in compute cycles. The latter has the opposite
trade-offs. The correct choice is always driven by which of these two
finite resources is in shorter supply.When faced with a "store versus compute" dilemma, always choose the one that involves the least "pain".
Listing 4.1
public class PegGameDos {
private static String blanks = " ";
public static void main( String[] args ) {
System.out.println();
char letter = 'A';
for (int row=0; row < 5; row++) {
System.out.print( blanks.substring( row*3 ) );
for (int column=0; column <= row; column++)
System.out.print( "<" + letter++ + "> " );
System.out.print( "\n\n" );
} } }
A two-dimensional array, with the second dimension growing in length, could have been chosen instead of a 1D array. This might seem like a more natural mapping of the problem space on to our solution space. The trade-off is having to specify an "x" and a "y" in order to designate a hole location. Down the road, when we have to think about representing/capturing a "move" with some data structure, two integers will be required instead of just one. Additionally, people are already comfortable talking about pins one through ten in the game of bowling. So, identifying pegs with the numbers one through fifteen, seems easier and more natural.
boolean[][] pegsPresent = { {true}, {true,true}, {true,true,true},
{true,true,true,true}, {true,true,true,true,true} };
for (int row=0; row < pegsPresent.length; row++) {
for (int column=0; column < pegsPresent[row].length; column++)
System.out.print( pegsPresent[row][column] + " " );
System.out.println();
}
// true
// true true
// true true true
// true true true true
// true true true true true
When a character is input by the user, it is converted to an array
index with the expression "(int) input.charAt(0) - 'a'". This converts
the character range 'a' through 'o' into the integer range 0 through
14. It is a common problem solving technique to transpose a problem
from its original domain (or perspective, or paradigm) to a seemingly
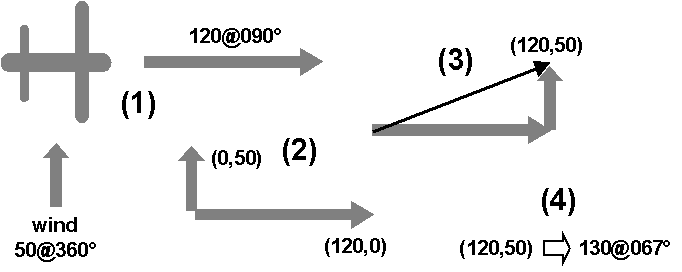
unnatural domain, in an effort to find a solution.An example is the addition of "vectors". A vector is a mathematical abstraction of a quantity that has both magnitude and direction. Wind is reported as a vector: 10 knots from the south. The polar coordinate system is natural for modeling vectors. Adding one vector to another in polar coordinates is hard. But - adding vectors that are modeled in the cartesian cooridinate system is easy.

Listing 4.2
public class PegGameDos {
private static boolean[] pegsPresent = new boolean[15];
private static String blanks = " ";
public static void display() {
System.out.println();
for (int i=0, row=0; row < 5; row++) {
System.out.print( blanks.substring( row*3 ) );
for (int col=0; col <= row; col++, i++)
if (pegsPresent[i])
System.out.print( "<" + (char)('A'+i) + "> " );
else
System.out.print( " " + (char)('a'+i) + " " );
System.out.print( "\n\n" );
} }
public static void main( String[] args ) {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
String input;
int peg;
while (true) {
display();
System.out.print( "Remove: " );
input = IOutils.getKeyboard();
if (input.equals(""))
break;
peg = (int) input.charAt(0) - 'a';
pegsPresent[peg] = ! pegsPresent[peg];
} } }
We might be tempted to eliminate all "duplicate" entries (i.e. jumping from position 1 to 4, or from position 4 to 1). But a move is not symmetric. Jumping from 1 to 4 means that positions 1 and 2 must be occupied, and position 4 must be empty. Whereas, jumping from 4 to 1 means that positions 4 and 2 are occupied, and position 1 is empty. So let's keep all 36 moves in our data structure.
A move can be captured with three integers: "from" position, "to" position, and "jumped" position. This means all possible moves can be captured in an int[36][3] data structure. See the jumpTable attribute in listing 4.3.
We could write a legalMove() function that returns true or false; but do we really need to know if a move request is not legal? What about writing an attemptMove() function that simply updates the pegsPresent attribute when the move request is legal, and does nothing otherwise?
The computation of the "from" and "to" positions in the main() of listing 4.3 generates values 0 through 14. The jumpTable attribute uses values 1 through 15. The "from" and "to" parameters passed to attemptMove() must be incremented before they can be used.
Given the specified "from" and "to" positions, how do we validate that they represent a valid jump? If we find those two values in the jump data structure, then we have part of our answer. How do we want to "search" the jump data structure? Sequentially stepping through the list of 36 moves is certainly easy, but is that choice prudent. Given that this search will only happen once for each user request, trying to identify an algorithm better than sequential search does not seem worth the effort.
The attributes common to great programmers are: hubris, resourcefulness, and laziness.
What we have so far is -
for (int i=0; i < jumpTable.length; i++) if (from == jumpTable[i][0] && to == jumpTable[i][1])But, is that all? If the "to" position has a peg sitting in it, then we can't honor the move request. The same is true if the "from" and "jumped" positions do not have pegs in them. This means the if condition needs to be extended.
Where is the knowledge of filled and empty positions? In the pegsPresent data structure. What do we need to use that data structure? An index, or offset, that represents a peg/hole position. Do we have any of that information at our disposal? Yes, in the {a,b,c} elements of the jumpTable data structure. What do we need to use that data structure? Two indexes, or offsets, that represent: a move, and a position within that move.
Once we have found the move data structure that corresponds to the user's request, then we need to check if: the "from" position is filled, the "jumped" position is filled, and the "to" position is vacant.
int fromPosition = jumpTable[i][0] - 1;
int jumpedPosition = jumpTable[i][2] - 1;
int toPosition = jumpTable[i][1] - 1;
if (... && pegsPresent[fromPosition] && pegsPresent[jumpedPosition]
&& ! pegsPresent[toPosition]) {
While this is more explicit than the implementation chosen in listing
4.3, perhaps it is more verbose than necessary - if - the more compact
code is well documented.The process we just went through to repeatedly ask: what do I know, and what do I need; could be characterized as a brute force approach, or "focusing on the trees". A lot of energy was invested in chapter 1 to discourage this kind of approach. Perhaps the reconciliation of this apparent contradiction would be to suggest: when you find yourself socked-in with a low ceiling and limited visibility, you should not be embarrassed to feel your way from one tree to the next.
"You can't get there from here" is fairly common advise. But, with enough tenacity, you can usually "find a way or make one." Consider the following cynical characterization of life.
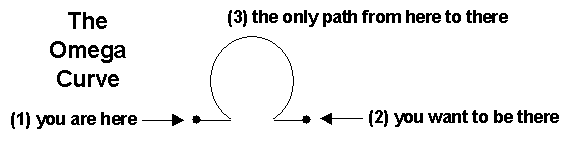
while (still short of a solution) {
what do I need?
what do I have?
where can I get to, from where I'm at?
}
public class PegGameDos {
private static boolean[] pegsPresent = new boolean[15];
private static String blanks = " ";
private static int jumpTable[][] = { {1,4,2}, {1,6,3},
{2,7,4}, {2,9,5},
/* {a,b,c} */ {3,8,5}, {3,10,6},
/* a = "from" position */ {4,6,5}, {4,1,2}, {4,11,7}, {4,13,8},
/* b = "to" position */ {5,14,9}, {5,12,8},
/* c = "jumped" position */ {6,4,5}, {6,13,9}, {6,15,10}, {6,1,3},
{7,2,4}, {7,9,8},
{8,3,5}, {8,10,9},
{9,2,5}, {9,7,8},
{10,8,9}, {10,3,6},
{11,13,12}, {11,4,7},
{12,5,8}, {12,14,13},
{13,11,12}, {13,15,14}, {13,6,9}, {13,4,8},
{14,12,13}, {14,5,9},
{15,13,14}, {15,6,10} };
public static void attemptMove( int from, int to ) {
from++; to++;
for (int i=0; i < jumpTable.length; i++)
if (from == jumpTable[i][0] && to == jumpTable[i][1]
&& pegsPresent[ jumpTable[i][0]-1 ] // if "from" position is filled
&& pegsPresent[ jumpTable[i][2]-1 ] // if "jumped" position is filled
&& ! pegsPresent[ jumpTable[i][1]-1 ]) { // if "to" position is vacant
pegsPresent[ jumpTable[i][0]-1 ] = false; // vacate the "from" position
pegsPresent[ jumpTable[i][2]-1 ] = false; // vacate the "jumped" position
pegsPresent[ jumpTable[i][1]-1 ] = true; // fill the "to" position
break;
} }
public static void display() {
System.out.println();
for (int i=0, row=0; row < 5; row++) {
System.out.print( blanks.substring( row*3 ) );
for (int col=0; col <= row; col++, i++)
if (pegsPresent[i])
System.out.print( "<" + ((char)('A'+i)) + ">" + " " );
else
System.out.print( " " + ((char)('a'+i)) + " " );
System.out.print( "\n\n" );
} }
public static void main( String[] args ) {
for (int i=0; i < pegsPresent.length; i++)
pegsPresent[i] = true;
String input;
int from, to;
display();
System.out.print( "Select initial hole: " );
input = IOutils.getKeyboard();
if (input.equals(""))
return;
from = (int) input.charAt(0) - 'a';
pegsPresent[from] = false;
while (true) {
display();
System.out.print( "Move (from to): " );
input = IOutils.getKeyboard();
if (input.equals(""))
break;
from = input.charAt(0) - 'a';
to = input.charAt(2) - 'a';
attemptMove( from, to );
} } }