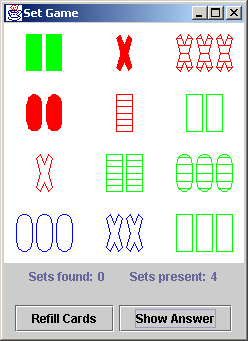
Set Puzzle
The puzzle is solved by finding sets of three cards that are all the
same, or all different, across four independent "facets" or
"dimensions". These dimensions are: number, shape, color, and fill.
Each of these dimensions has three possible values. Number may be: one,
two, or three; color may be: red, green, or blue; shape may be: rectangle, X,
or O; and fill may be: open, striped, or solid.
|
Example sets:
|
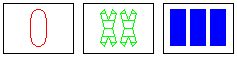 |
a SET
same: [none]
different: number, color, shape, fill
|
 |
a SET
same: number, color, shape
different: fill
|
 |
a SET
same: number, shape
different: color, fill
|
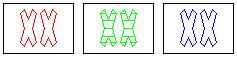 |
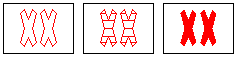
NOT a set
same: number, shape
different: color
wrong: fill |
|
To make it a set, one of the open fills needs to
be solid, or the striped fill needs to be open.
|
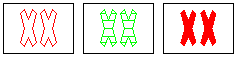
 |
a SET
same: shape
different: color, number, fill
|
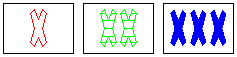
 |
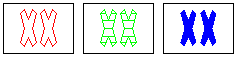
NOT a set
same: shape, number
different: fill
wrong: color |
|
To make it a set, one of the red colors needs to
be blue, or the green color needs to be red.
|
How many cards would you expect in a Set deck?
How would you uniquely identify each card?
Can you "compute" the value of each of the four
dimensions, or, does it need to be "stored"?
public static void compute_components( int card, int[] components ) {
components[0] = card % 3;
components[1] = card % 9 / 3;
components[2] = card % 27 / 9;
components[3] = card / 27;
}
What kind of algorithm will give us a decision on whether
3 cards constitute a set?
card1 0 0 1 1 2 2 0 0 1 2
card2 0 1 1 2 2 0 1 0 1 2
card3 1 1 2 2 0 0 2 0 1 2
set? no no no no no no yes yes yes yes
Above are all combinations of three 3-valued variables.
Is a pattern or source of leverage evident?
Here is an implementation ...
boolean is_a_set( int[] selected_cards ) {
int[][] cards_and_components = new int[3][4];
for (int i=0; i < 3; i++)
compute_components( selected_cards[i], cards_and_components[i] );
for (int sum, i=0; i < 4; i++) {
sum = 0;
for (int j=0; j < 3; j++)
sum += cards_and_components[j][i];
// If any of the 4 sums is not evenly divisible by 3, then the 3 cards do not form a set
if (sum % 3 != 0)
return false;
}
return true;
}
What kind of algorithm is necessary and sufficient to
compute all the sets present in an array of 12 cards?
What is the equation for "all combinations of X things
taken Y at a time"?
Here is an implementation ...
int number_of_sets = 0;
for (int i=0; i < cards_showing.length - 2; i++)
for (int j=i+1; j < cards_showing.length - 1; j++)
for (int k=j+1; k < cards_showing.length; k++) {
test_set[0] = cards_showing[i];
test_set[1] = cards_showing[j];
test_set[2] = cards_showing[k];
if (is_a_set( test_set )) {
number_of_sets++;
answer.append(test_set[0]+1).append(' ');
answer.append(test_set[1]+1).append(' ');
answer.append(test_set[2]+1).append(" ");
} }
return number_of_sets;
How about supplying the "view" component (Java GUI code)
and having the student design the "model" component (game engine)?






