Cracker Barrel Peg Game

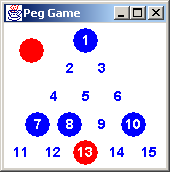
The Cracker Barrel Peg Game consists of fifteen holes arranged in a triangle, and fourteen pegs. The object is to remove pegs by jumping until one peg remains. The player chooses where the empty hole is positioned before play is begun.

In the parallel examples to the right, the player starts the game by selecting the 1 position as the blank spot. She then jumps the 6 peg over the 3 peg and into the 1 position, and removes the 3 peg. Next, the 15 peg jumps over the 10 peg and into the 6 position, and the 10 peg is removed.

How should the notion of "move" be implemented?

How should you validate whether a requested move is legal?

Is this an algorithm issue or a data structure issue?

Is it necessary to create an enormous "case" statement to test every possible move?

Can legal moves be "computed", and therefore handled with a single piece of code?

 


             <A>

          <B>   <C>

       <D>   <E>   <F>

    <G>   <H>   <I>   <J>

 <K>   <L>   <M>   <N>   <O> 

 Select initial hole: a



              a

          <B>   <C>

       <D>   <E>   <F>

    <G>   <H>   <I>   <J>

 <K>   <L>   <M>   <N>   <O>

 Move (from to): f a



             <A>

          <B>    c

       <D>   <E>    f

    <G>   <H>   <I>   <J>

 <K>   <L>   <M>   <N>   <O>

 Move (from to): o f



             <A>

          <B>    c

       <D>   <E>   <F>

    <G>   <H>   <I>    j

 <K>   <L>   <M>   <N>    o

 Move (from to):
After the game is implemented, it would be nice if it could be extended so that the Peg Game player is warned if a requested move has no hope of resulting in a winning game. Consider the game to the right. The correct sequence of moves are: 7 to 9, 13 to 6, 10 to 3, and 1 to 6. If the player chooses 13 to 4 instead; then 7 can jump to 2, and 1 to 4. That would result in two pegs remaining: 4 and 10. So, our game needs to sound an alarm (e.g. draw a red dot) when the user asks for the 13 to 4 move.

    

How can you enumerate and test every possible pathway through the game?

How do people do it when they play the real game?

Given the game beginning presented above, here is a hierarchical representation of all possible moves for the sequence of moves: start with the empty spot at position 1, 6-1, 15-6.

Here is an alternate representation that uses a list of lists to enumerate all possible moves. To make the next move, the last move of the last list is chosen, and it is replaced with a new list of all new possible moves. When a non-winning game is identified, the algorithm (either human or computer) "backtracks" to the next move that could have previously been selected (instead of the move that WAS selected, but has since been found to be a dead-end).

Here is an alternate representation that demonstrates four non-solutions. After 7 moves, the board has reached the state shown at the top. Four moves are now possible. If the 3-8 move is chosen, then two moves are possible. The 13-4 move eventually leads to three pegs remaining, and the 1-4 move leads to an end state of five pegs.