
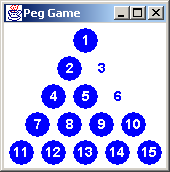

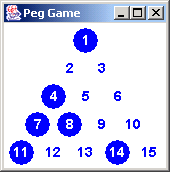
 It would be nice if our Peg Game application could keep the player from
painting herself into a corner. Take the board to the right. The
correct sequence of moves are: 7 to 9, 13 to 6, 10 to 3, and 1 to 6.
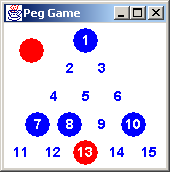
If the player chooses 13 to 4 instead; then 7 can jump to 2, and 1 to
4. That would result in two pegs remaining: 4 and 10. So, our game
needs to sound an alarm (e.g. draw a red dot) when the user asks for
the 13 to 4 move.
It would be nice if our Peg Game application could keep the player from
painting herself into a corner. Take the board to the right. The
correct sequence of moves are: 7 to 9, 13 to 6, 10 to 3, and 1 to 6.
If the player chooses 13 to 4 instead; then 7 can jump to 2, and 1 to
4. That would result in two pegs remaining: 4 and 10. So, our game
needs to sound an alarm (e.g. draw a red dot) when the user asks for
the 13 to 4 move.Consider a strategy that uses a stack to record all possible moves. Solutions are found by: pushing all "possible moves" on the stack, popping the first entry off the stack, executing that move, testing if a single peg remains, if so - a solution was found, if not - repeat the process.
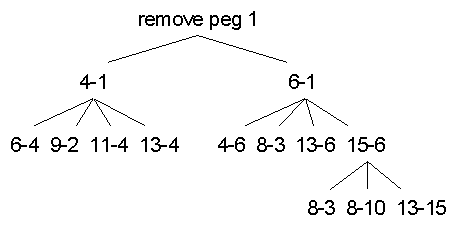
Consider the following first 2 moves ...



Here is a "tree" representation of "possible moves" ...
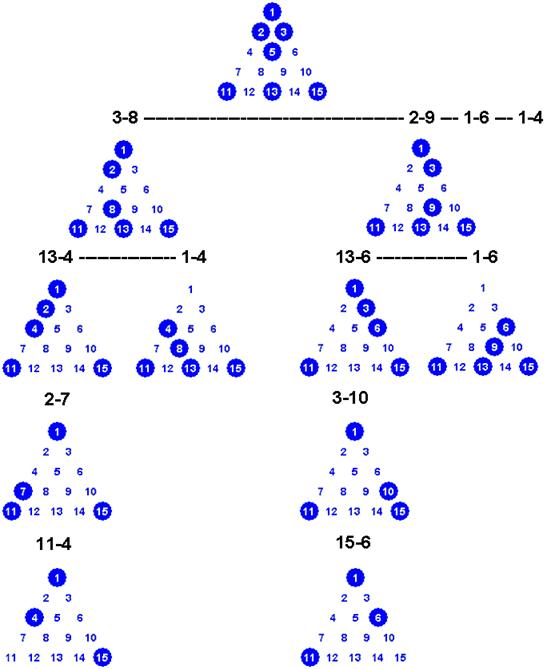
A graphical representation is optimal for carbon-based intelligence (i.e. people), but it doesn't map directly to silicon-based intelligence (computers). If we had a representation that was more sequential in nature (like a computer's memory), then we could perhaps kill two birds with one stone: discuss a solution strategy for the problem, and, lay the foundation for the eventual algorithm.
Another issue with the graphical representation above is overhead. Modeling all the possible moves of a game as separate nodes in a fully populated tree consumes a lot of memory. As we come up with a more sequential encoding of the game, is there a way we could accommodate some kind of "just in time" representation? The motivation is to maintain as little game state as possible.
Instead of building a full-grown tree, perhaps a step-by-step "list of lists" representation will provide sufficient bookkeepping for: testing one specific game, backtracking to alternate games, and ultimately testing every possible game. How about the following procedure and data structure?
remove peg 1 (4-1 6-1) (4-1 (4-6 8-3 13-6 15-6) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 8-3) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 14-5) ) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 (3-8 3-10 12-14 2-9) ) ) ) ) (4-1 (4-6 8-3 13-6 (8-10 13-15 (3-10 13-15 (3-8 3-10 12-14 (3-10 7-2 12-14) ) ) ) ) )The board now looks like -

To eliminate some clutter, let's focus only on the last list of moves. The steps remain: move, generate, replace.
(3-10 7-2 12-14) 9 pegs left (3-10 7-2 (6-13 7-2 14-5 3-10) ) 8 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 10-8) ) ) 7 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 7-9) ) ) ) 6 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 (14-5) ) ) ) ) 5 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 ((4-6)) ) ) ) ) 4 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2 (( )) ) ) ) ) 3 pegs leftAt this point, the pegs remaining are 1, 6, 11; and there are no more possible moves.
We've hit a dead-end, and need to backtrack to an alternate pathway. Lets add a new step 3 to our procedure.
The top line below looks like the fourth line above - except - the 7-9 move at the end has been removed. We are ready to proceed forward again. As each last move of the last list is executed, there is only one possible move on the board. So, each replacement is performed with a list composed of a single move.
(3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (7-2) ) ) ) 6 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((1-4)) ) ) ) 5 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (((4-13))) ) ) ) 4 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((((14-12)))) ) ) ) 3 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 (((((11-13))))) ) ) ) 2 pegs left (3-10 7-2 (6-13 7-2 14-5 (7-2 14-5 ((((())))) ) ) ) 1 peg left
We now have a "sequential" representation of our puzzle. It should give us a good start on a search algorithm. Notice how the list demonstrates last in, first out behavior.
Our 4-step procedure seems to suggest a loop where step 4 feeds back to step 2. Would recursion be preferable?